Skupina B

1

Správná odpověď macimálně 13 bodů, nesmyslná -4 body

Zadání

Proveďte analýzu třídícího algoritmu BubbleSort daného následujícím pseudokódem.

$\textbf{Vstup\hspace{0.3cm}: }$ Pole $\textit{A}[0..\textit{n} - 1]$
$\textbf{Výstup\hspace{0.075cm}: }$ Vrací true, pokud jsou všechny prvky unikátní, jinak vrací false

1 $\textbf{for}$ $\textit{i}$ $\gets$ 0 $\textbf{to}$ $\textit{n} - 2$ $\textbf{do}$
2 $\hspace{0.5cm}\textbf{for}$ $\textit{j}$ $\gets$ $i + 1$ $\textbf{to}$ $\textit{n} - 1$ $\textbf{do}$
3 $\hspace{1.0cm}\textbf{if}$ $\textit{A}[i] = \textit{A}[j]$ $\textbf{then}$
4 $\hspace{1.5cm}$ $\textbf{return}$ $\textit{false}$;
5 $\hspace{1.0cm}\textbf{end}$
6 $\hspace{0.5cm}\textbf{end}$
7 $\textbf{end}$
8 $\textbf{return}$ $\textit{true}$

Vaším úkolem provést analýzu algoritmu. Očekávají se odpovědi na následující otázky:
(a) ^{_{(1 bod)}} Volba parametru reprezentujícího velikost vstupu.
(b) ^{_{(1 bod)}} Nalezení základních operací algoritmu.
(c) ^{_{(3 body)}} Je nutné u daného algoritmu rozlišovat nejhorší, průměrný a nejlepší případ? Nebo tyto případy splývají? Na čem závisí rozhodnutí? Poznámka: Pokud by bylo nutné zkoumat více případů,bude stačit, když vypracujete řešení pro nejhorší případ.
(d) ^{_{(3 body)}} Sestavení rovnic, vyjadřujících počet základních operací vykonaných algoritmem v závislostina velikosti vstupu.
(e) ^{_{(3 body)}} Zjednodušení rovnic sestavených v předcházejícím bodě.
(f) ^{_{(2 body)}} Stanovení řádového růstu složitosti algoritmu.

Řešení

(a) n (počet prvnů v poli A)
(b) porovnání dvou prvků$A[i] = A[j]$
(c) V tomto případě není nutné rozlišovat, protože procházíme vždy všechny okolní prvky pole. Jeho složitost tudíž závisí na velikosti vstupu.
(d)

$$\begin{align*} \displaystyle\sum^{n-2}_{i=0}\sum^{n-1}_{j=i+1} &= \sum^{n-2}_{i=0}[(n-1)-(i+1)+1]\\ &= \sum^{n-2}_{i=0}n-1-i-1+1\\ &= \sum^{n-2}_{i=0}n-1-i\\ &= \sum^{n-2}_{i=0}(n-1) - \sum^{n-2}_{i=0}i \\ &= (n - 1) - \sum^{n-2}_{i=0}i - \dfrac{(n-2)(n-1)}{2}\\ &= {(n-1)}^2-\dfrac{(n-2)(n-1)}{2}\\ &= \dfrac{(n-1)n}{2} \end{align*}$$

(e) $\dfrac{1}{2}n$
(f) $O(n^2)$

2

Správná odpověď maximálně 5 bodů, nesmyslná -1 bod

Zadání

Je dána následující posloupnost písmen: LHRVNXJDTFBP. Písmena z této posloupnosti byla postupně, v pořadí jak jsou zapsána, vložena do binárního vyhledávacího stromu. Nakreslete výsledný strom. Jen pro připomenutí, abeceda vypadá takto: ABCDEFGHIJKLMNOPQRSTUVWXYZ.

Řešení

$$\begin{array}{cccccccccccccccccccccccccccccc} &&&&&&&&&&&&&& \text{L} &&&&&&&&&&&&&& \\ &&&&&&&&&&&& \swarrow &&&& \searrow &&&&&&&&&&&& \\ &&&&&&&&&&& \text{H} &&&&&&& \text{R} &&&&&&&& \\ &&&&&&&&&& \swarrow && \searrow &&&& \swarrow &&&& \searrow &&&&&& \\ &&&&&&&&& \text{D} &&&& \text{J} && \text{N} &&&&&& \text{V} &&&&&&& \\ &&&&&&&& \swarrow && \searrow &&&&&& \searrow &&&& \swarrow && \searrow &&&&&& \\ &&&&&&& \text{B} &&&& \text{F} &&&&&& \text{P} && \text{T} &&&& X && \end{array}$$

3

Správná odpověď maximálně 5 bodů, nesmyslná -2 body

Zadání

Máte dánu funkci $f(n) = 3n^4 - 8n^3 - 5n^2 - 5n - 11$. Formálně matematicky dokažte, zda platí $f(n)\in O(n^3)$ nebo $f(n)\notin O(n^3)$

Řešení

$$\begin{align*} \displaystyle \lim_{n\to\infin}\dfrac{3n^4-8n^3-5n^2-5n-11}{n^3} &= \lim_{n\to\infin}\dfrac{\not{n^3}(3n^{^{\nearrow^{\normalsize^{\infin}}}}-8^{^{\nearrow^{\normalsize^{c}}}}-\dfrac{5}{n}^{^{\nearrow^{\normalsize^{0}}}}-\dfrac{5}{n^2}^{^{\nearrow^{\normalsize^{0}}}}-\dfrac{11}{n^3}^{^{\nearrow^{\normalsize^{0}}}})}{\not{n^3}} \\ &= \underline{\infin} \end{align*}$$

,takže $\underline{\underline{f(n)\not\in O(n^3)}}$

4

Správná odpověď maximálně 5 bodů, nesmyslná -1 bod

Zadání

Máte dán neorientovaný graf, viz obrázek vpravo. Na tento graf aplikujte algoritmus průchodu grafem do šířky. Počáteční vrchol pro průchod grafem je vrchol K. Zapište vrcholy grafu v tom pořadí, jakém je algoritmus průchodu grafem do šířky postupně navštívil (prošel, zpracoval,...). Poznámka: Sousední vrcholy k danému vrcholu předávejte k dalšímu zpracování vždy v abecedním pořadí. Předpokládejme například, že algoritmus právě zpracovává vrchol M. A dále předpokládejme, že s tímto vrcholem sousedí vrcholy Q, W a R. Sousední vrcholy předáme k dalšímu zpracování v pořadí Q, R a W.

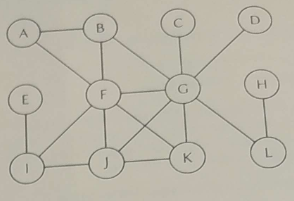
Řešení

BFS = KFGJABICDLEH

5

Správná odpověď maximálně 3 body, nesmyslná -1 bod

Zadání

Máme dán orientovaný acyklický graf, viz obrázek vpravo. Na tento graf aplikujte algoritmus topologiského třídění. Zapište vrcholy grafu seřazené algoritmem topologického třídění.

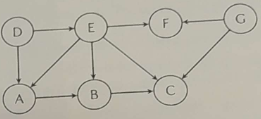
Řešení

Postup: vrcholy, do kterých nevedou cesty $\Rightarrow$ DGEFABC

6

Správná odpověď maximálně 9 bodů, nesmyslná -3 body

Zadání

Jednou z klasických úloh v informatice je Problém batohu (Knapsack Problem). Vaším úkolem je:

(a) ^{_{(3 body)}} nejprve definovat problém samotný, dále
(b) ^{_{(3 body)}} vysvětlete řešení tohoto problému pomocí strategie řešení hrubou silou (brute force strategy), a nakonec
(c) ^{_{(3 body)}} odhadněte časovou složitost řešení.

Poznámka: V odpovědi se můžete omezit na dvourozměrný prostor.

Řešení

(a) Problém batohu, je optimalizační problém, kde je dán batoh s omezenou kapacitou a soubor předmětů, přičemž každý předmět má svou váhu a hodnotu. Cílem je vybrat takovou kombinaci předmětů, která maximalizuje celkovou hodnotu při splnění omezení nosnosti.
(b) Algoritmus u Brute force postupuje rekurzivně a pro každý předmět má 2 možnosti: buď přidá, nebo ne. Algoritmus projde všechny předměty a vybere optimální kombinaci.
(c) Pomocí Brute force je exponenciální, tedy $O(n^2)$.