Skupina A

1

Správná odpověď macimálně 13 bodů, nesmyslná -4 body

Zadání

Proveďte analýzu třídícího algoritmu BubbleSort daného následujícím pseudokódem.

$\textbf{Vstup\hspace{0.3cm}: }$ Dvě čtvercové matice $\textit{A}$ a $\textit{B}$ řádu $n$
$\textbf{Výstup\hspace{0.075cm}: }$ Čtvercová matice $\textit{C}$ řádu $n$, kde $\textit{C} = \textit{AB}$

1 $\textbf{for}$ $\textit{i}$ $\gets$ 0 $\textbf{to}$ $\textit{n} - 1$ $\textbf{do}$
2 $\hspace{0.5cm}\textbf{for}$ $\textit{j}$ $\gets$ $0$ $\textbf{to}$ $\textit{n} - 1$ $\textbf{do}$
3 $\hspace{1.0cm}\textit{C}[i,j] \gets 0$;
4 $\hspace{1.0cm}\textbf{for}$ $\textit{j}$ $\gets$ $0$ $\textbf{to}$ $\textit{n} - 1$ $\textbf{do}$
5 $\hspace{1.5cm}$ $\textit{C}[i,j]$ $\gets$ $\textit{C}[i,j] + \textit{A}[i,k] * \textit{B}[k,j]$;
6 $\hspace{1.0cm}\textbf{end}$
7 $\hspace{0.5cm}\textbf{end}$
8 $\textbf{end}$
9 $\textbf{return}$ $\textit{C}$;

Vaším úkolem provést analýzu algoritmu. Očekávají se odpovědi na následující otázky:
(a) ^{_{(1 bod)}} Volba parametru reprezentujícího velikost vstupu.
(b) ^{_{(1 bod)}} Nalezení základních operací algoritmu.
(c) ^{_{(3 body)}} Je nutné u daného algoritmu rozlišovat nejhorší, průměrný a nejlepší případ? Nebo tyto případy splývají? Na čem závisí rozhodnutí? Poznámka: Pokud by bylo nutné zkoumat více případů,bude stačit, když vypracujete řešení pro nejhorší případ.
(d) ^{_{(3 body)}} Sestavení rovnic, vyjadřujících počet základních operací vykonaných algoritmem v závislostina velikosti vstupu.
(e) ^{_{(3 body)}} Zjednodušení rovnic sestavených v předcházejícím bodě.
(f) ^{_{(2 body)}} Stanovení řádového růstu složitosti algoritmu.

Řešení

(a) n (počet řádků u čtvercových matic je stejný jako počet sloupců)
(b) Základní operace jsou:

• ‎Inicializace matice $C$ na hodnotu 0, pro každý prvek jedna operace (Iterace pomocí i,j)
• ‎Násobení matic $A$ a $B$ a přičtení hodnoty $C$ pro daný prvek (Přes iteraci k) [//]: # (End list) (c) V tomto případě není nutné rozlišovat, protože procházíme vždy všechny okolní prvky pole. Jeho složitost tudíž závisí na velikosti vstupu.
  (d)

$$\displaystyle M(n) = \sum^{n-1}_{i=0}\sum^{n-1}_{j=0}\sum^{n-1}_{k=0}1$$

(e)

$$\begin{align*} \displaystyle M(n) &= \sum^{n-1}_{i=0}\sum^{n-1}_{j=0}\sum^{n-1}_{k=0}1\\ &= \sum^{n-1}_{i=0}\sum^{n-1}_{j=0}n\\ &= \sum^{n-1}_{i=0}n^2\\ &= n^3 \end{align*}$$

(f) $O(n^3)$

2

Správná odpověď maximálně 5 bodů, nesmyslná -1 bod

Zadání

Je dána následující posloupnost písmen: JDPHTRBXNLFV. Písmena z této posloupnosti byla postupně, v pořadí jak jsou zapsána, vložena do binárního vyhledávacího stromu. Nakreslete výsledný strom. Jen pro připomenutí, abeceda vypadá takto: ABCDEFGHIJKLMNOPQRSTUVWXYZ.

Řešení

$$\begin{array}{cccccccccccccccccccccccccccccc} &&&&&&&&&&&&&& \text{J} &&&&&&&&&&&&&& \\ &&&&&&&&&&&& \swarrow &&&& \searrow &&&&&&&&&&&& \\ &&&&&&&&&&& \text{D} &&&&&&& \text{P} &&&&&&&& \\ &&&&&&&&&& \swarrow && \searrow &&&& \swarrow &&& \searrow &&&&&&& \\ &&&&&&&&& \text{B} &&&& \text{H} && \text{N} &&&&& \text{T} &&&&&&&& \\ &&&&&&&&&&&& \swarrow && \swarrow &&&&& \swarrow && \searrow &&&&&&& \\ &&&&&&&&&&& \text{F} && \text{L} &&&&& \text{R} &&&& \text{X} &&& \\ &&&&&&&&&&&&&&&&&&&&& \swarrow &&&& \\ &&&&&&&&&&&&&&&&&&&& \text{V} &&&&& \end{array}$$

3

Správná odpověď maximálně 5 bodů, nesmyslná -2 body

Zadání

Máte dánu funkci $f(n) = 12n^4 - 3n^3 + n^2 - 7n - 8$. Formálně matematicky dokažte, zda platí $f(n)\in \Omega(n^3)$ nebo $f(n)\notin \Omega(n^3)$

Řešení

$$\begin{align*} \displaystyle \lim_{n\to\infin}\dfrac{12n^4-3n^3+n^2-7n-8}{n^3} &= \lim_{n\to\infin}\dfrac{\not{n^3}(12n^{^{\nearrow^{\normalsize^{\infin}}}}-3^{^{\nearrow^{\normalsize^{c}}}}+\dfrac{1}{n}^{^{\nearrow^{\normalsize^{0}}}}-\dfrac{7}{n^2}^{^{\nearrow^{\normalsize^{0}}}}-\dfrac{8}{n^3}^{^{\nearrow^{\normalsize^{0}}}})}{\not{n^3}} \\ &= \underline{\infin} \end{align*}$$

,takže $\underline{\underline{f(n)\in \Omega(n^3)}}$

4

Správná odpověď maximálně 5 bodů, nesmyslná -1 bod

Zadání

Máte dán neorientovaný graf, viz obrázek vpravo. Na tento graf aplikujte algoritmus průchodu grafem do šířky. Počáteční vrchol pro průchod grafem je vrchol F. Zapište vrcholy grafu v tom pořadí, jakém je algoritmus průchodu grafem do šířky postupně navštívil (prošel, zpracoval,...). Poznámka: Sousední vrcholy k danému vrcholu předávejte k dalšímu zpracování vždy v abecedním pořadí. Předpokládejme například, že algoritmus právě zpracovává vrchol M. A dále předpokládejme, že s tímto vrcholem sousedí vrcholy Q, W a R. Sousední vrcholy předáme k dalšímu zpracování v pořadí Q, R a W.

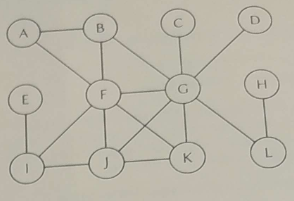
Řešení

BFS = FABGJICDLEH

5

Správná odpověď maximálně 3 body, nesmyslná -1 bod

Zadání

Máme dán orientovaný acyklický graf, viz obrázek vpravo. Na tento graf aplikujte algoritmus topologiského třídění. Zapište vrcholy grafu seřazené algoritmem topologického třídění.

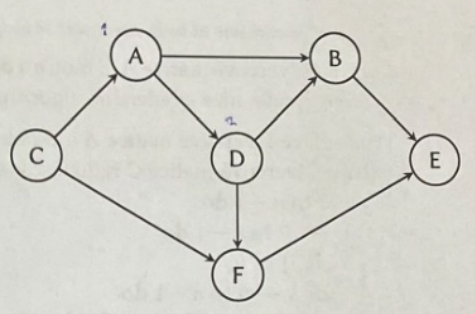
Řešení

Postup: vrcholy, do kterých nevedou cesty $\Rightarrow$ CADFBE

6

Správná odpověď maximálně 9 bodů, nesmyslná -3 body

Zadání

Jednou z klasických úloh v informatice je Problém obchodního cestujícího (Traveling Salesman Problem). Vaším úkolem je:

(a) ^{_{(3 body)}} nejprve definovat problém samotný, dále
(b) ^{_{(3 body)}} vysvětlete řešení tohoto problému pomocí strategie řešení hrubou silou (brute force strategy), a nakonec
(c) ^{_{(3 body)}} odhadněte časovou složitost řešení.

Poznámka: V odpovědi se můžete omezit na dvourozměrný prostor.

Řešení

(a) Kombinaristický problém, kde je cílem najít nejkratsí cestu pro obchodního cestujícího, který musí navštívit určený počet míst a vrátit se zpět di výchozího bodu. Cílem je tedy minimalizovat délku cesty, přičemž musí navštívit všechna uřčená místa jen jednou.
(b) Pomocí Brute force se řeší tak, že vyzkouší systematicky všchny kombinace měst, které začínají a končí ve stejném městě. Následně vybere cestu s nejkratší délkou, která představuje optimální řešení.
(c) Časová složitost je $O(n!)$, kde $n$ je počet měst, exponenciálně roste čas s rostoucím počtem měst.